서론
이전 시간에는 데이터 과학의 프로세스 중에서 데이터 수집에 해당하는 표본추출의 종류가 무엇이 있는지 알아보았습니다. 대부분의 분석이 전수조사를 할 수 없기 때문에 우리는 모집단에서 표본을 추출하여 표본의 통계량을 확인한 뒤, 모집단의 모수를 추정하는 방식을 사용한다고 했는데요. 오늘은 데이터 가공에 앞서 변수와 척도의 개념에 대해서 공부해 보도록 하겠습니다.

1 : 데이터 과학 공부하기 - 통계학 기초(표본 추출)
변수의 종류
데이터 과학은 변수와 변수의 관계를 밝혀내는 활동입니다. 그렇다면 변수란 무엇일까요? 변수는 말 그대로 값이 변하는 수라고 생각하면 됩니다. 상수와는 반대되는 개념으로 값이 변할 수 있는 성질을 가지고 있는 건데요. 변수도 여러 가지 종류가 존재합니다.
가감 승계(+, -, *, /)로 연산을 하는 것이 의미가 있으면 양적변수, 없으면 질적변수로 구분할 수 있습니다. 양적변수 안에서도 정숫값만 취할 수 있으면 이산 변수(discrete variable), 연속적인 모든 실숫값을 취할 수 있으면 연속변수(continuous variable)로 구분됩니다.
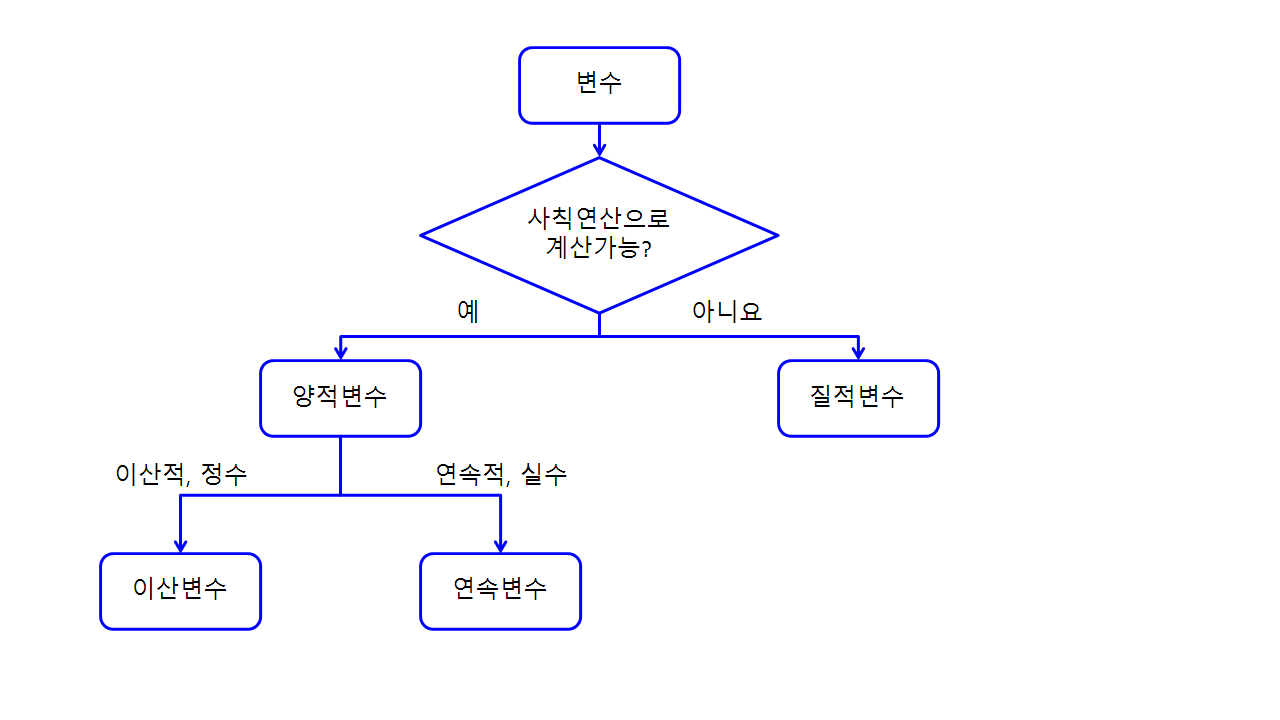
- 질적변수는 성별, 종교, 지지 정당과 같이 숫자로 변환하더라도 계산이 불가능한 변수입니다.
- 이산 변수는 인구 수, 득점 개수, 판매량과 같이 정수를 가지는 변수입니다.
- 연속변수는 키, 몸무게, 땅 면적과 같이 크기나 길이, 양과 같은 연속적인 수(실수)를 가지는 변수입니다.
변수 간의 관계
변수끼리도 서로 관계가 존재합니다. 그중에서 중요한 것은 단연 인과관계, 상관관계, 독립 관계라고 할 수 있습니다. 이 세 가지 관계는 다른 공부를 하면서도 많이 등장했습니다. 글자 그대로 직관적인 의미를 가지고 있어서 외우기도 쉽습니다. 그 외에 의사 관계, 양방향적 인과관계, 조절 관계, 매개 관계 등이 있습니다. 저는 깊게 들어가지 않고 세 가지 관계에 대해서만 기술하겠습니다.

상관관계는 변수끼리 서로 상관성이 있는 관계입니다. 확실히 해야 할 것은 인과관계와 헷갈리면 안 된다는 것인데요. 서로 관련이 있을 뿐이지 원인과 결과가 되지는 않습니다. 변수 간의 상관성을 나타내는 지표로 상관계수가 있습니다. 정확히는 피어슨 상관계수로, R^2로 표기합니다. 이는 0~1까지의 실수를 가지는데 보통 0.7 이상을 상관성이 깊다고 본다고 합니다. 1이면 서로 똑같은 방향성을 띠는 것이고 0이면 아예 관련이 없다는 의미겠죠. 변수 A가 증가(+) 또는 감소(-) 할 때, 변수 B도 같이 증가 또는 감소하는지 알려주는 지표라고 생각하면 쉽습니다.
독립 관계는 변수끼리 서로 상관성이 없는 관계입니다. 상관관계와 반대되는 개념이라고 생각하면 쉽습니다. 변수가 서로 독립적인 관계로, 영향을 전혀 주고받지 않는 경우에 독립관계라고 합니다.
※ 독립 관계인 변수끼리는 상관계수가 0이지만, 상관계수가 0인 변수끼리 독립 관계가 아닐 수 있다.
인과관계는 어떤 변수가 원인이 되고 다른 변수가 결과가 되는 관계입니다. 이때 원인이 되는 변수를 독립변수라고 하고 결과가 되는 변수를 종속변수라고 합니다. 독립변수의 변화는 종속변수의 변화에 영향을 끼칩니다. 독립변수끼리는 서로 독립 관계여야 합니다.
척도의 종류
평소에 척도라는 단어를 종종 들어보셨을 텐데요. 척도는 측정하고자 하는 대상을 수치화하기 위해 사용되는 방법이라고 합니다. 쉽게 말해서 우리가 수집한 데이터를 분석하려면 수치화 시켜야 하는데, 그 규칙을 판단하는 기준이 척도가 되는 것입니다. 척도는 다음과 같이 4가지 종류가 있습니다.

변수가 질적 변수인지 양적 변수인지에 따라 질적 척도와 양적 척도로 나뉩니다. 질적 척도는 속성값을 범주로 나타내는지 순위로 나타내는지에 따라 명목 척도와 서열 척도로 나뉩니다. 양척 척도는 절대적 기준인 영점이 존재하는가에 따라 등간 척도와 비율 척도로 나뉩니다. 이렇게 추상적인 얘기를 들으면 이해가 잘 안됩니다. (저만 그런가요) 우선 이렇게 이해해 볼까요? 명목→서열 →등간 →비율 순으로 가지는 정보의 양이 많아집니다. 명목 척도가 가장 적은 정보를 가지고 비율 척도가 가장 많은 정보를 가집니다. 왜 그럴까요?
명목 척도(nominal scale)는 조사대상의 속성이나 범주를 구분하기 위한 목적으로 만들어졌습니다. 쉽게 말해서 '서로 다르다'는 정보만 가진 것입니다. 성별이나 혈액형과 같이 서로 다르긴 다르지만 서로 간에 순서, 거리 및 원점의 개념이 없기 때문에 숫자로 변환해도 순서나 크기에 의미가 없습니다. 따라서 사칙연산 같은 계산도 의미가 없고 서로 다름만 구분하면 되므로 가진 정보의 양이 가장 적게 되는 것입니다.
서열 척도(ordinal scale)는 조사대상의 속성 크기를 측정하여 대상 간의 순서 관계를 측정하는 척도입니다. 쉽게 말해서 명목 척도에서 순서가 추가된 개념입니다. 서로 다르고 순서를 가지는 관계를 표현하기에 적합하겠죠? 예를 들어 한 학급의 성적 등수는 학생마다 서로 다르며 순서를 가지므로 서열 척도에 해당합니다.
등간 척도(interval scale)는 조사대상 간의 크기 차이를 비교할 수 있습니다. 서열 척도에서 상대적 크기가 추가된 개념입니다. 등간 척도는 한 학급의 시험 점수를 예시로 들 수 있습니다. 서열 척도의 예시로 학급의 성적 등수는 1등, 2등, 3등... 의 정보만 가지고 있었습니다. 반면에 등간 척도의 예시로 시험 점수는 0점부터 100점까지 정숫값을 가지므로 서로 가감(+, -) 하는 것이 가능합니다. 따라서 서로 간의 차이를 알 수 있습니다.
비율 척도(ratio scale)는 조사대상 간의 절대적 비율을 계산할 수 있습니다. 등간 척도에서 절대적 크기가 추가된 개념입니다. 즉, 가감 승계(+, -, *, /)가 모두 가능하다는 의미가 됩니다. 서로 곱하고 나눌 수 있기 때문에 비율을 알 수 있겠죠? 예시로 키, 몸무게 등이 있습니다. 몸무게가 80kg인 사람은 40kg인 사람보다 2배 무겁다고 말할 수 있습니다.
| 종류 | 세부 분류 | 포함 정보 | |||
| 질적 척도 | 명목 척도 | 범주 | |||
| 서열 척도 | 범주 | 순서 | |||
| 양적 척도 | 등간 척도 | 범주 | 순서 | 상대적 크기 | |
| 비율 척도 | 범주 | 순서 | 상대적 크기 | 절대적 크기 | |
( [데이터 분석가가 반드시 알아야 할 모든 것] 책의 내용이 너무 좋아서 표를 인용했습니다.)
'컴퓨터공학 > 데이터과학' 카테고리의 다른 글
| 데이터 과학 공부하기 - 통계학 기초(확률 분포, 중심극한정리) (2) | 2024.11.24 |
|---|---|
| 데이터 과학 공부하기 - 통계학 기초(기술 통계) (4) | 2024.11.23 |
| 데이터 과학 공부하기 - 통계학 기초(표본 추출) (4) | 2024.11.20 |